Secant variety

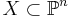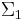In Algebraic Geometry, the Zariski closure of the union of the secant lines to an embedded projective variety $X\subset\mathbb{P}^n$ is the first secant variety to $X$ . It is usually denoted $\Sigma_1$ .

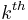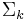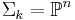The $k^{th}$ secant variety is the Zariski closure of the union of the linear spaces spanned by collections of k+1 points on $X$ . It is usually denoted $\Sigma_k$ . Unless $\Sigma_k=\mathbb{P}^n$ , it is always singular along 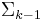$\Sigma_{k-1}$ , but may have other singular points.

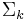If $X$ has dimension d, the dimension of $\Sigma_k$ is at most kd+d+k.

References

Joe Harris, Algebraic Geometry, A First Course, (1992) Springer-Verlag, New York. ISBN 0-387-97716-3